Bài 30 trang 67 SGK Toán 7 tập 2 | Myphamthucuc.vn

Bài 4: Tính chất ba đường trung tuyến của tam giác

Bài 30 (trang 67 SGK Toán 7 tập 2)

 Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G’ sao cho G là trung điểm của AG’.

a) So sánh các cạnh của tam giác BGG’ với các đường trung tuyến của tam giác ABC.

b) So sánh các đường trung tuyến của tam giác BGG’ với các cạnh của tam giác ABC.

Lời giải: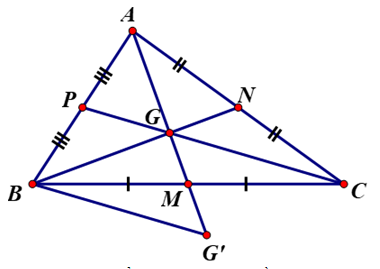

a) Gọi trung điểm BC, CA, AB lần lượt là M, N, P.

⇒ AM, BN, CP là các đường trung tuyến và G là trọng tâm của ΔABC

Theo tính chất đường trung tuyến của tam giác ta có:

GB = 2/3.BN (1)

GA = 2/3.AM, mà GA = GG’ (do G là trung điểm của AG’) ⇒ GG’ = 2/3.AM (2)

GM=1/2.AG, mà AG=GG’ ⇒ GM=1/2.GG’ ⇒ M là trung điểm của GG’ hay GM = GM’ .

Xét ΔGMC và ΔG’MB có:

GM = G’M (chứng minh trên)

 MC = MB

⇒ ΔGMC = ΔG’MB (c.g.c)

⇒ GC = G’B (hai cạnh tương ứng).

Mà CG = 2/3.CP (tính chất đường trung tuyến) ⇒ G’B = 2/3.CP (3)

Từ (1), (2), (3) ta có : GG’ = 2/3.AM , GB = 2/3.BN, G’B = 2/3.CP.

b) Gọi I, K lần lượt là trung điểm của BG, BG’.

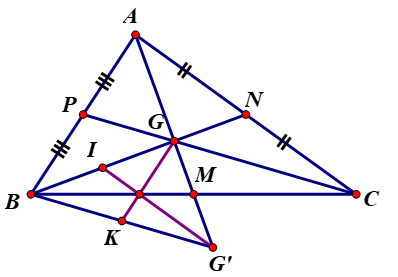
Xem toàn bộ Giải Toán 7: Luyện tập trang 67