Giải Toán 12: Bài 1 trang 23-24 SGK Giải tích 12
Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Bài 1 trang 23-24 SGK Giải tích 12:
Tính giá trị lớn nhất và nhỏ nhất của hàm số:
a) y = x3 – 3x2 – 9x + 35 trên các đoạn [-4; 4] và [0; 5] ;
b) y = x4 – 3x2 + 2 trên các đoạn [0; 3] và [2; 5] ;
c) 
trên các đoạn [2 ; 4] và [-3 ; -2] ;
d) 
trên đoạn [-1 ; 1].
Lời giải:
a) TXĐ: D = R.
y’ = 3x2 – 6x – 9;
y’ = 0 ⇔ x = –1 hoặc x = 3.
+ Xét hàm số trên đoạn [-4; 4] :
y(-4) = -41 ;
y(-1) = 40 ;
y(3) = 8
y(4) = 15.
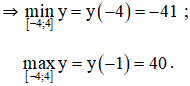
+ Xét hàm số trên [0 ; 5].
y(0) = 35 ;
y(3) = 8 ;
y(5) = 40.
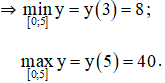
b) TXĐ: D = R
y’ = 4x3 – 6x
y’ = 0 ⇔ 2x.(2x2 – 3) = 0 ⇔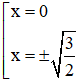 
+ Xét hàm số trên [0 ; 3] :
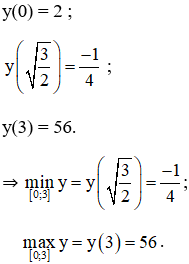
+ Xét hàm số trên [2; 5].
y(2) = 6;
y(5) = 552.
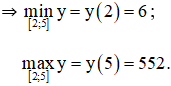
c) TXĐ: D = (-∞; 1) ∪ (1; +∞)
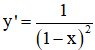> 0 với ∀ x ∈ D.
⇒ hàm số đồng biến trên (-∞; 1) và (1; +∞).
⇒ Hàm số đồng biến trên [2; 4] và [-3; -2]
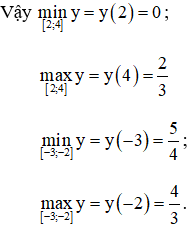
d) TXĐ: D = (-∞; 5/4]
với ∀ x ∈ (-∞; 5/4)
⇒ Hàm số nghịch biến trên (-∞; 5/4)
⇒ Hàm số nghịch biến trên [-1; 1]
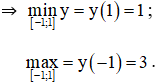
Kiến thức áp dụng
Quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f(x) trên [a; b].
+ Tìm các điểm xi trên khoảng (a; b) sao cho tại đó f’(xi) = 0 hoặc không xác định.
+ Tính f(a); f(xi); f(b).
+ Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:
Nếu hàm số đồng biến trên [a; b] thì
Nếu hàm số nghịch biến trên [a; b] thì
Có thể bạn quan tâm
Bài viết hay nhất
Câu 10. Tại sao phải dạy học tích hợp? Chủ trương dạy học tích hợp có gì mới? Những thuận lợi, khó khăn và cách khắc phục khi thực hiện dạy học tích hợp? | Myphamthucuc.vn
Mối quan hệ biện chứng giữa cái chung và cái riêng? Vận dụng ý nghĩa phương pháp luận trong giải quyết mối quan hệ trên để phân tích mối quan hệ giữa chủ nghĩa Mác-Lênin với thực tiễn cách mạng Việt Nam? | Myphamthucuc.vn
Câu 11. Tại sao phải thực hiện dạy học phân hóa? Chủ trương dạy học phân hóa trong CT mới có gì khác CT hiện hành? Những thuận lợi và khó khăn trong việc thực hiện dạy học phân hóa hiện và cách khắc phục? | Myphamthucuc.vn
Tư tưởng Đất Nước của Nhân dân trong Đất nước của Nguyễn Khoa Điềm
Các Kiểm Tra Hạn Sử Dụng Của Kem Chống Nắng Skin Aqua Nhật Bản
Bài thơ “Ngắm trăng” được sáng tác trong hoàn cảnh nào?
Câu hỏi ôn tập bài Sau phút chia li chọn lọc chi tiết
Phân tích tâm trạng nhân vật Liên khi chờ tàu năm 2023
Giới thiệu về Ngô Gia văn phái năm 2023
Kem Dưỡng Estee Lauder Thật Giả Qua Các Dung Tích, So Sánh Và Nhận Biết Serum Advance Night Repair
Nhân vật Mị sau khi về làm dâu nhà thống lí Pá Tra trong Vợ chồng A Phủ
Phân tích bức tranh tứ bình trong bài Nhớ rừng của Thế Lữ năm 2023
Viết thư cho Cô giáo cũ nhân ngày 20/11 năm 2023
Soạn bài Vừa nhắm mắt vừa mở cửa sổ