Giải Toán 11: Bài 4 trang 53 SGK Hình học 11 | Myphamthucuc.vn
Bài 1: Đại cương về đường thẳng và mặt phẳng
Bài 4 trang 53 SGK Hình học 11
Cho bốn điểm A, B, C và D không đồng phẳng. Gọi GA, GB, GC, GD lần lượt là trọng tâm của các tam giác BCD, CDA, ADB, ACB. Chứng minh rằng AGA, BGB, CGC, DGD đồng qui.
Lời giải
Hướng dẫn
Gọi G = AGA ∩ BGB; G′= AGA ∩ CGC; G′′= AGA ∩ DGD, chứng minh các tỉ số 
.
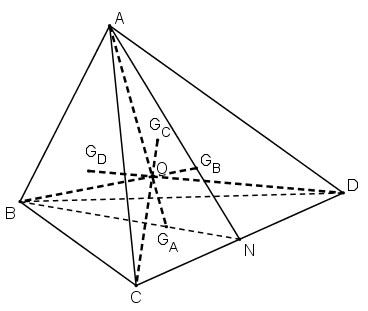
Gọi N là trung điểm CD.
+ GA là trọng tâm ΔBCD
⇒ GA ∈ trung tuyến BN ⊂ (ANB)
⇒ AGA ⊂ (ANB)
GB là trọng tâm ΔACD
⇒ GB ∈ trung tuyến AN ⊂ (ANB)
⇒ BGB ⊂ (ANB).
Trong (ANB): AGA không song song với BGB
⇒ AGA cắt BGB tại O
+ Chứng minh tương tự: BGB cắt CGC; CGC cắt AGA.
+ CGC không nằm trong (ANB) ⇒ AGA; BGB; CGC không đồng phẳng.
⇒ AGA; BGB; CGC đồng quy tại O
+ Chứng minh hoàn toàn tương tự: AGA; BGB; DGD đồng quy tại O
Vậy AGA; BGB ; CGC; DGD đồng quy tại O (đpcm).
Xem toàn bộ Giải Toán 11: Bài 1. Đại cương về đường thẳng và mặt phẳng
Có thể bạn quan tâm
Bài viết hay nhất
Câu 10. Tại sao phải dạy học tích hợp? Chủ trương dạy học tích hợp có gì mới? Những thuận lợi, khó khăn và cách khắc phục khi thực hiện dạy học tích hợp? | Myphamthucuc.vn
Mối quan hệ biện chứng giữa cái chung và cái riêng? Vận dụng ý nghĩa phương pháp luận trong giải quyết mối quan hệ trên để phân tích mối quan hệ giữa chủ nghĩa Mác-Lênin với thực tiễn cách mạng Việt Nam? | Myphamthucuc.vn
Câu 11. Tại sao phải thực hiện dạy học phân hóa? Chủ trương dạy học phân hóa trong CT mới có gì khác CT hiện hành? Những thuận lợi và khó khăn trong việc thực hiện dạy học phân hóa hiện và cách khắc phục? | Myphamthucuc.vn
Tư tưởng Đất Nước của Nhân dân trong Đất nước của Nguyễn Khoa Điềm
Các Kiểm Tra Hạn Sử Dụng Của Kem Chống Nắng Skin Aqua Nhật Bản
Bài thơ “Ngắm trăng” được sáng tác trong hoàn cảnh nào?
Câu hỏi ôn tập bài Sau phút chia li chọn lọc chi tiết
Phân tích tâm trạng nhân vật Liên khi chờ tàu năm 2023
Giới thiệu về Ngô Gia văn phái năm 2023
Kem Dưỡng Estee Lauder Thật Giả Qua Các Dung Tích, So Sánh Và Nhận Biết Serum Advance Night Repair
Nhân vật Mị sau khi về làm dâu nhà thống lí Pá Tra trong Vợ chồng A Phủ
Phân tích bức tranh tứ bình trong bài Nhớ rừng của Thế Lữ năm 2023
Viết thư cho Cô giáo cũ nhân ngày 20/11 năm 2023
Soạn bài Vừa nhắm mắt vừa mở cửa sổ