Câu hỏi Ôn tập chương 3 Toán 7 tập 2 phần Hình Học | Myphamthucuc.vn
Ôn tập chương III – Phần Hình học
Câu hỏi ôn tập
Câu hỏi ôn tập 1 trang 86 Toán 7 tập 2
Cho tam giác ABC. Hãy viết kết luận của hai bài toán sau về quan hệ giữa góc và cạnh đối diện trong một tam giác.
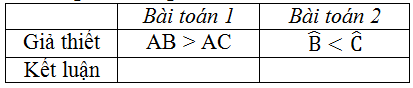
Lời giải
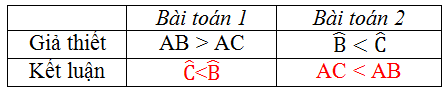
Câu hỏi ôn tập 2 trang 86 Toán 7 tập 2
Từ điểm A không thuộc đường thẳng d, kẻ đường vuông góc AH, các đường xiên AB, AC đến đường thẳng d. Hãy điền dấu (>, <) vào các chỗ trống (…) dưới đây cho đúng:
a) AB … AH; AC … AH.
b) Nếu HB … HC thì AB … AC.
c) Nếu AB … AC thì HB … HC.
Lời giải
a) AB > AH; AC > AH.
b) Nếu HB > HC thì AB > AC.
hoặc Nếu HB < HC thì AB < AC.
c) Nếu AB > AC thì HB > HC.
hoặc Nếu AB < AC thì HB < HC.
Câu hỏi ôn tập 3 trang 86 Toán 7 tập 2
Cho tam giác DEF. Hãy viết bất đẳng thức về quan hệ giữa các cạnh của tam giác này.
Lời giải
Với ΔDEF ta có các bất đẳng thức và quan hệ giữa các cạnh là:
DE < EF + DF
DF < EF + DE
EF < DE + DF
DF – EF < DE < DF + EF (với DF > EF)
Câu hỏi ôn tập 4 trang 86 Toán 7 tập 2
Hãy ghép 2 ý ở 2 cột để được khẳng định đúng: …
Lời giải
Ghép a-d’ ; b –a’, c-b’, d-c’
Trong một tam giác
a – d’ đường phân giác xuất phát từ đỉnh A – là đoạn thẳng có hai mút là đỉnh A và giao điểm của cạnh BC với tia phân giác của góc A.
b – a’ đường trung trực ứng với cạnh BC – là đường vuông góc với cạnh BC tại trung điểm của nó.
c – b’ đường cao xuất phát từ đỉnh A – là đoạn vuông góc kẻ từ A đến đường thẳng BC.
d – c’ đường trung tuyến xuất phát từ đỉnh A – là đoạn thẳng nối A với trung điểm của cạnh BC.
Câu hỏi ôn tập5 trang 86 Toán 7 tập 2
Hãy ghép 2 ý ở 2 cột để được khẳng định đúng: …
Lời giải
Ghép a-b’, b-a’, c-d’, d-c’
Trong một tam giác
a – b’ trọng tâm – là điểm chung của ba đường trung tuyến
b – a’ trực tâm – là điểm chung của ba đường cao
c – d’ điểm (nằm trong tam giác) cách đều ba cạnh – là điểm chung của ba đường phân giác
d – c’ điểm cách đều ba đỉnh – là điểm chung của ba đường trung trực
Câu hỏi ôn tập 6 trang 86 Toán 7 tập 2
a) Hãy nêu tính chất trọng tâm của một tam giác; các cách xác định trọng tâm.
b) Bạn Nam nói: “Có thể vẽ được một tam giác có trọng tâm ở bên ngoài tam giác”. Bạn Nam nói đúng hay sai? Tại sao?
Lời giải
a)– Trọng tâm của một tam giác có tính chất :
“Trọng tâm cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó.”
– Các cách xác định trọng tâm:
+ Cách 1: Vẽ 2 đường trung tuyến ứng với 2 cạnh tùy ý, rồi xác định giao điểm của 2 đường trung tuyến đó.
+ Cách 2: Vẽ 1 đường trung tuyến của tam giác. Chia độ dài đường trung tuyến thành 3 phần bằng nhau rồi xác định một điểm cách đỉnh 2 phần bằng nhau.
b)Nam nói sai
Không thể vẽ được 1 tam giác có trọng tâm ở bên ngoài tam giác vì đường trung tuyến qua 1 đỉnh của tam giác và trung điểm 1 cạnh trong tam giác nên đường trung tuyến phải nằm giữa 2 cạnh của một tam giác tức nằm ở bên trong của một tam giác nên 3 đường trung tuyến cắt nhau chỉ có thể nằm bên trong của tam giác.
Câu hỏi ôn tập 7 trang 86 Toán 7 tập 2
Những tam giác có ít nhất một đường trung tuyến đồng thời là đường phân giác, đường trung trực, đường cao?
Lời giải
Tam giác có ít nhất 1 đường trung tuyến đồng thời là đường phân giác, đường trung trực, đường cao là tam giác cân, tam giác vuông cân.
Câu hỏi ôn tập 8 trang 86 Toán 7 tập 2
Những tam giác nào có trọng tâm đồng thời là trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh?
Lời giải
Tam giác có trọng tâm đồng thời là trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh là tam giác đều.
Xem toàn bộ Giải Toán 7: Ôn tập chương 3 phần Hình Học
Có thể bạn quan tâm
Bài viết hay nhất
Mối quan hệ biện chứng giữa cái chung và cái riêng? Vận dụng ý nghĩa phương pháp luận trong giải quyết mối quan hệ trên để phân tích mối quan hệ giữa chủ nghĩa Mác-Lênin với thực tiễn cách mạng Việt Nam? | Myphamthucuc.vn
Câu 10. Tại sao phải dạy học tích hợp? Chủ trương dạy học tích hợp có gì mới? Những thuận lợi, khó khăn và cách khắc phục khi thực hiện dạy học tích hợp? | Myphamthucuc.vn
Câu 11. Tại sao phải thực hiện dạy học phân hóa? Chủ trương dạy học phân hóa trong CT mới có gì khác CT hiện hành? Những thuận lợi và khó khăn trong việc thực hiện dạy học phân hóa hiện và cách khắc phục? | Myphamthucuc.vn
Tư tưởng Đất Nước của Nhân dân trong Đất nước của Nguyễn Khoa Điềm
Các Kiểm Tra Hạn Sử Dụng Của Kem Chống Nắng Skin Aqua Nhật Bản
Bài thơ “Ngắm trăng” được sáng tác trong hoàn cảnh nào?
Câu hỏi ôn tập bài Sau phút chia li chọn lọc chi tiết
Phân tích tâm trạng nhân vật Liên khi chờ tàu năm 2023
Giới thiệu về Ngô Gia văn phái năm 2023
Kem Dưỡng Estee Lauder Thật Giả Qua Các Dung Tích, So Sánh Và Nhận Biết Serum Advance Night Repair
Nhân vật Mị sau khi về làm dâu nhà thống lí Pá Tra trong Vợ chồng A Phủ
Bộ đề Đọc hiểu Trường ca những người đi tới biển hay nhất thi THPT Quốc gia | Myphamthucuc.vn
Phân tích bức tranh tứ bình trong bài Nhớ rừng của Thế Lữ năm 2023
Viết thư cho Cô giáo cũ nhân ngày 20/11 năm 2023
