Bài 61 trang 83 SGK Toán 7 tập 2 | Myphamthucuc.vn

Bài 9: Tính chất ba đường cao của tam giác

Bài 61 (trang 83 SGK Toán 7 tập 2)

Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.

a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.

b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB và HAC.

Lời giải: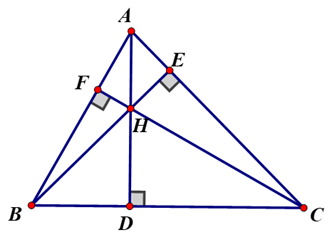

Gọi D, E, F là chân các đường vuông góc kẻ từ A, B, C của ΔABC.

⇒ AD ⟘ BC, BE ⟘ AC, CF ⟘ AB.

a) Xét ΔHBC có :

AD ⊥ BC suy ra AD là đường cao từ H đến BC.

BA ⊥ HC tại F suy raBA là đường cao từ B đến HC

CA ⊥ BH tại E suy raCA là đường cao từ C đến HB.

AD, BA, CA cắt nhau tại A suy raA là trực tâm của ΔHCB.

b) Tương tự :

+ Trực tâm của ΔHAB là điểm C (C là giao điểm của 3 đường cao : CF, AC, BC)

+ Trực tâm của ΔHAC làđiểm B (B là giao điểm của 3 đường cao : BE, AB, CB)

Xem toàn bộ Giải Toán 7: Bài 9. Tính chất ba đường cao của tam giác