Bài 42 trang 73 SGK Toán 7 tập 2 | Myphamthucuc.vn

Bài 6: Tính chất ba đường phân giác của tam giác

Bài 42 (trang 73 SGK Toán 7 tập 2)

Chứng minh định lí: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân. Gợi ý: Trong ΔABC, nếu AD là đường trung tuyến vừa là đường phân giác thì kéo dài AD một đoạn DA, sao cho DA₁ = AD.

Lời giải: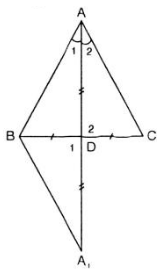

– Giả sử ∆ABC có AD là trung tuyến đồng thời là tia phân giác của góc BAC

Ta cần chứng minh ∆ABC cân tại A.

Kéo dài AD một đoạn DA₁ = AD.

– Xét ∆ADB và ∆A₁DC có

AD = DA₁ (cách vẽ)

BD = CD (do D là trung điểm BC)

Suy ra ∆ADB = ∆A₁DC (c.g.c)

⇒ ∆ACA₁ cân tại C ⇒ AC = A₁C (2)

Từ (1) và (2) ⇒ AB = AC.

Vậy ∆ABC cân tại A

Nhận xét: Nếu tam giác có 1 đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.

Xem toàn bộ Giải Toán 7: Luyện tập trang 73