Lý thuyết Toán 8: Ôn tập chương 3 Hình học | Myphamthucuc.vn

Ôn tập chương 3

1. Đoạn thẳng tỉ lệ

a) Định nghĩa

AB,CD tỉ lệ với A’B’,C’D’ ⇔ AB/CD = A’B’/C’D’.

b) Tính chất

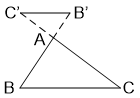
AB/CD = A’B’/C’D’

⇒ 

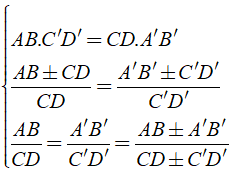
2. Định lý Ta – lét thuận và đảo

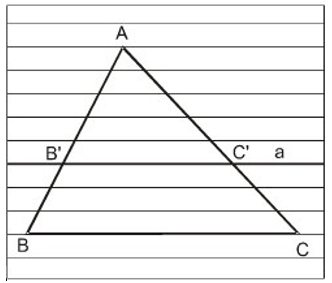
Khi a//BC ⇔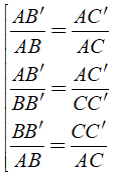 

3. Hệ quả định lý Ta – lét trong tam giác

Ta có a//BC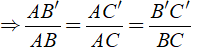 

4. Tính chất đường phân giác trong tam giác

a) Phân giác góc trong

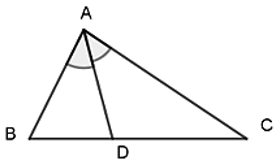
Tổng quát: ΔABC, AD là đường phân giác của góc BACˆ (D∈BC)

Ta có: DB/DC = AB/AC hay DB/AB = DC/AC

b) Phân giác góc ngoài

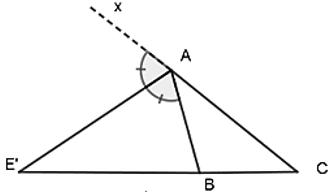
AE’ là phân giác của góc BAxˆ (AB ≠ AC)

Ta có: AB/AC = E’B/E’C hay E’B/AB = E’C/AC

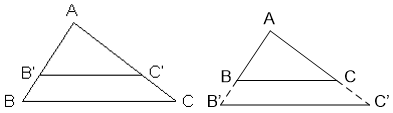
5. Tam giác đồng dạng

– Hai tam giác được gọi là đồng dạng với nhau nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.

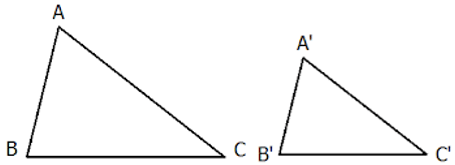
– Tam giác ABC gọi là đồng dạng với tam giác A’B’C’ nếu:

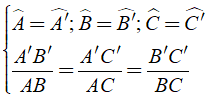
Kí hiệu: Δ ABC ∼ Δ A’B’C’

Tỉ số cách cạnh tương ứng A’B’/AB = A’C’/AC = B’C’/BC = k được gọi là tỉ số đồng dạng

6. Các trường hợp bằng nhau và trường hợp đồng dạng của hai tam giác

a) Các trường hợp bằng nhau

+ A’B’ = AB;B’C’ = BC và A’C’ = AC ⇒ Δ ABC = Δ A’B’C'(c – c – c)

+ A’B’ = AB; B’C’ = BC và Bˆ = B’ˆ ⇒ Δ ABC = Δ A’B’C'(c – g – c).

+ Aˆ = A’ˆ; Bˆ = B’ˆ và A’B’ = AB ⇒ ΔABC = ΔA’B’C'(g – c – g).

b) Các trường hợp đồng dạng

+ A’B’/AB = A’C’/AC = B’C’/BC ⇒ ΔABC ∼ ΔA’B’C’ (c – c – c).

+ A’B’/AB = B’C’/BC và Bˆ = B’ˆ ⇒ Δ ABC ∼ Δ A’B’C’ (c – g – c).

+ Aˆ = A’ˆ và Bˆ = B’ˆ ⇒ ΔABC ∼ ΔA’B’C’ (g – g).

7. Trường hợp đồng dạng của tam giác vuông ABC và A’B’C’ (với Aˆ= A’ˆ= 90^o)

+ A’B’/AB = A’C’/AC.

+ Bˆ = B’ˆ hoặc Cˆ = C’ˆ.

+ A’B’/AB = B’C’/BC.

8. Mở rộng

Nếu hai tam giác đồng dạng với nhau thì:

+ Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.

+ Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.

+ Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.

+ Tỉ số các chu vi bằng tỉ số đồng dạng.

+ Tỉ số các diện tích bằng bình phương tỉ số đồng dạng.

Xem thêm Giải Toán 8: Ôn tập chương 3