Giải Toán 8: Bài 51 trang 33 SGK Toán 8 tập 2
Ôn tập chương 3 (Câu hỏi – Bài tập)
Bài 51 (trang 33 SGK Toán 8 tập 2)
Giải các phương trình sau bằng cách đưa về phương trình tích:
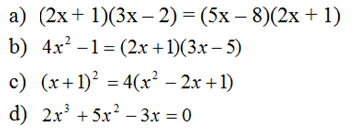
Lời giải:
a) (2x + 1)(3x – 2) = (5x – 8)(2x + 1)
⇔ (2x + 1)(3x – 2) – (5x – 8)(2x + 1) = 0
⇔ (2x + 1).[(3x – 2) – (5x – 8)] = 0
⇔ (2x + 1).(3x – 2 – 5x + 8) = 0
⇔ (2x + 1)(6 – 2x) = 0
⇔ 2x + 1 = 0 hoặc 6 – 2x = 0
+ 2x + 1 = 0 ⇔ 2x = -1 ⇔ x = -1/2.
+ 6 – 2x = 0 ⇔ 6 = 2x ⇔ x = 3.
Vậy phương trình có tập nghiệm: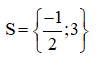
b) 4x2– 1 = (2x + 1)(3x – 5)
⇔ 4x2 – 1 – (2x + 1)(3x – 5) = 0
⇔ (2x – 1)(2x + 1) – (2x + 1)(3x – 5) = 0
⇔ (2x + 1)[(2x – 1) – (3x – 5)] = 0
⇔ (2x + 1)(2x – 1 – 3x + 5) = 0
⇔ (2x + 1)(4 – x) = 0
⇔ 2x + 1= 0 hoặc 4 – x = 0
+ 2x + 1 = 0 ⇔ 2x = -1 ⇔ x = -1/2.
+ 4 – x = 0 ⇔ x = 4.
Vậy phương trình có tập nghiệm: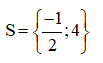
c) (x + 1)2= 4(x2– 2x + 1)
⇔ (x + 1)2 = 4(x – 1)2
⇔ 4(x – 1)2 – (x + 1)2 = 0 (hằng đẳng thức)
⇔ [2(x – 1) – (x + 1)].[2(x – 1) + (x + 1)] = 0
⇔ (2x – 2 – x – 1)(2x – 2 + x + 1) = 0
⇔ (x – 3)(3x – 1) = 0
⇔ x – 3 = 0 hoặc 3x – 1 = 0
+ x – 3 = 0 ⇔ x = 3.
+ 3x – 1 = 0 ⇔ 3x = 1 ⇔ x = 1/3.
Vậy phương trình có tập nghiệm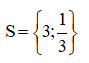
d) 2x3+ 5x2– 3x = 0
⇔ x(2x2 + 5x – 3) = 0
⇔ x.(2x2 + 6x – x – 3) = 0
⇔ x. [2x(x + 3) – (x + 3)] = 0
⇔ x.(2x – 1)(x + 3) = 0
⇔ x = 0 hoặc 2x – 1 = 0 hoặc x + 3 = 0
+ 2x – 1 = 0 ⇔ 2x = 1 ⇔ x = 1/2.
+ x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm: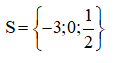
Tham khảo toàn bộ: Giải Toán 8



















