Giải Toán 8: Bài 27 trang 22 SGK Toán 8 tập 2 | Myphamthucuc.vn

Bài 5 Phương trình chứa ẩn ở mẫu

Bài 27 (trang 22 SGK Toán 8 tập 2)

Giải các phương trình:

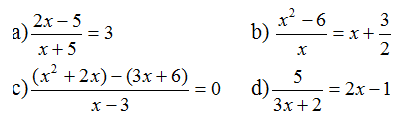
Lời giải:

a) Điều kiện xác định: x ≠ -5.

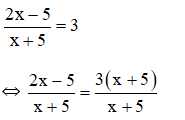
2x – 5 = 3(x + 5)

⇔ 2x – 5 = 3x + 15

⇔ -5 – 15 = 3x – 2x

⇔ x = -20 (thỏa mãn điều kiện xác định).

Vậy phương trình có tập nghiệm S = {-20}.

b) Điều kiện xác định: x ≠ 0.

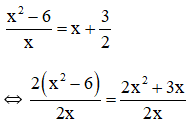
2(x² – 6) = 2x² + 3x

⇔ 2x² – 12 – 2x² – 3x = 0

⇔ 3x = 12

⇔ x = 4 (Thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm S = {4}.

c) Điều kiện xác định: x ≠ 3.

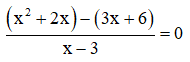
⇔ x² + 2x – (3x + 6) = 0

⇔ x(x + 2) – 3(x + 2) = 0

⇔ (x – 3)(x + 2) = 0

⇔ x – 3 = 0 hoặc x + 2 = 0

+ x – 3 = 0 ⇔ x = 3 (Không thỏa mãn đkxđ)

+ x + 2 = 0 ⇔ x = -2 (Thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm S = {-2}.

d) Điều kiện xác định: x ≠ -2/3.

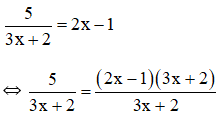
⇔ 5 = (2x – 1)(3x + 2)

⇔ 2x.3x – 3x.1 + 2x.2 – 2.1 = 5

⇔ 6x² – 3x + 4x – 2 = 5

⇔ 6x² + x – 7 = 0.

⇔ 6x² – 6x + 7x – 7 = 0

(Tách để phân tích vế trái thành nhân tử)

⇔ 6x(x – 1) + 7(x – 1) = 0

⇔ (6x + 7)(x – 1) = 0

⇔ 6x + 7 = 0 hoặc x – 1 = 0

+ 6x + 7 = 0 ⇔ 6x = – 7 ⇔ x = -7/6 (thỏa mãn đkxđ)

+ x – 1 = 0 ⇔ x = 1 (thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm:

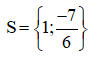
Tham khảo toàn bộ: Giải Toán 8