Giải Toán 12: Bài 2 trang 18 SGK Giải tích 12 | Myphamthucuc.vn

Bài 2: Cực trị của hàm số

Bài 2 trang 18 SGK Giải tích 12: 

Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau:

a) y = x⁴ – 2x² + 1 ;

b) y = sin2x – x

c) y = sinx + cosx ;

d) y = x⁵ – x³ – 2x + 1

Lời giải:

a) TXĐ: D = R.

+ y’ = 4x³ – 4x

y’ = 0 ⇔ 4x(x² – 1) = 0 ⇔ x = 0 hoặc x = ±1.

+ y” = 12x² – 4

y”(0) = -4 < 0 ⇒ x = 0 là điểm cực đại của hàm số.

y”(1) = 8 > 0 ⇒ x = 1 là điểm cực tiểu của hàm số.

y”(-1) = 8 > 0 ⇒ x = -1 là điểm cực tiểu của hàm số.

b) TXĐ: D = R

+ y’ = 2cos2x – 1;

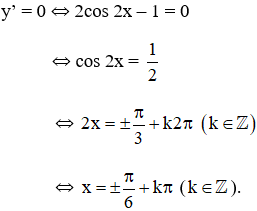
+ y” = -4.sin2x

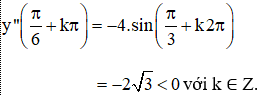
⇒  (k ∈ Z) là các điểm cực đại của hàm số.

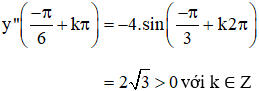
⇒  (k ∈ Z) là các điểm cực tiểu của hàm số.

c) TXĐ: D = R

+ y’ = cos x – sin x.

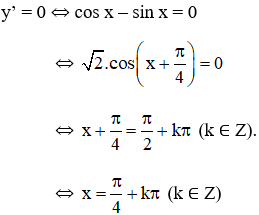
+ y’’ = -sin x – cos x = 

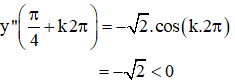
⇒  là các điểm cực đại của hàm số.

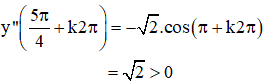
⇒  là các điểm cực tiểu của hàm số.

d) TXĐ: D = R

+ y’= 5x⁴ – 3x² – 2

y’ = 0 ⇔ 5x⁴ – 3x² – 2 = 0

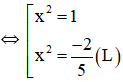
⇔ x = ±1.

+ y” = 20x³ – 6x

y”(-1) = -20 + 6 = -14 < 0

⇒ x = -1 là điểm cực đại của hàm số.

y”(1) = 20 – 6 = 14 > 0

⇒ x = 1 là điểm cực tiểu của hàm số.