Giải Toán 12: Bài 1 trang 9 SGK Giải tích 12 | Myphamthucuc.vn
Bài 1: Sự đồng biến, nghịch biến của hàm số
Bài 1 trang 9 SGK Giải tích 12:
Xét sự đồng biến, nghịch biến của hàm số:
a) y = 4 + 3x – x2
b)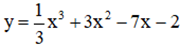 
c) y = x4 – 2x2 + 3
d) y = -x3 + x2 – 5
Lời giải:
Kiến thức áp dụng
Xét sự đồng biến, nghịch biến của hàm số y = f(x).
Bước 1: Tìm tập xác định .
Bước 2: Tính đạo hàm y’. Tìm các giá trị của x để f’(x) = 0 hoặc f’(x) không xác định.
Bước 3: Sắp xếp các giá trị của x ở trên theo thứ tự tăng dần và lập bảng biến thiên.
Lưu ý: Dấu của f’(x) trong một khoảng trên bảng biến thiên chính là dấu của f’(x) tại một điểm x0 bất kì trong khoảng đó. Do đó, ta chỉ cần lấy một điểm x0 bất kì trong khoảng đó rồi xét xem f’(x0) dương hay âm.
Bước 4: Kết luận về khoảng đồng biến và nghịch biến của hàm số.
a) Tập xác định : D = R
y’ = 3 – 2x
y’ = 0 ⇔ 3 – 2x = 0 ⇔ x = 
Ta có bảng biến thiên:
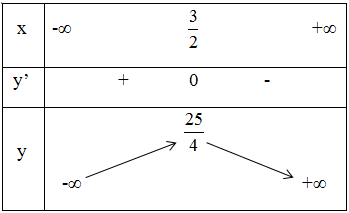
Vậy hàm số đồng biến trong khoảng (-∞; 3/2) và nghịch biến trong khoảng (3/2 ; + ∞).
b) Tập xác định : D = R
y’ = x2 + 6x – 7
y’ = 0 ⇔ x = -7 hoặc x = 1
Ta có bảng biến thiên:
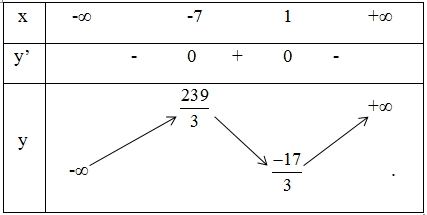
Vậy hàm số đồng biến trong các khoảng (-∞ ; -7) và (1 ; +∞); nghịch biến trong khoảng (-7; 1).
c) Tập xác định: D = R
y’= 4x3 – 4x.
y’ = 0 ⇔ 4x3 – 4x = 0 ⇔ 4x.(x – 1)(x + 1) = 0 ⇔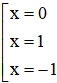 
Bảng biến thiên:
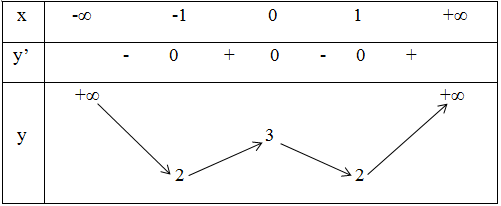
Vậy hàm số nghịch biến trong các khoảng (-∞ ; -1) và (0 ; 1); đồng biến trong các khoảng (-1 ; 0) và (1; +∞).
d) Tập xác định: D = R
y’= -3x2 + 2x
y’ = 0 ⇔ -3x2 + 2x = 0 ⇔ x.(-3x + 2) = 0 ⇔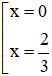 
Bảng biến thiên:
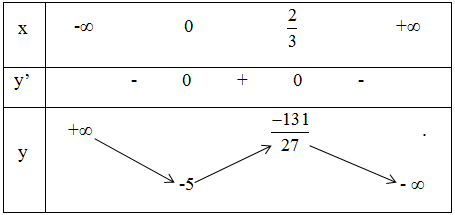
Vậy hàm số nghịch biến trong các khoảng (-∞ ; 0) và (2/3 ; + ∞), đồng biến trong khoảng (0 ; 2/3).
Có thể bạn quan tâm
Bài viết hay nhất
Câu 10. Tại sao phải dạy học tích hợp? Chủ trương dạy học tích hợp có gì mới? Những thuận lợi, khó khăn và cách khắc phục khi thực hiện dạy học tích hợp? | Myphamthucuc.vn
Mối quan hệ biện chứng giữa cái chung và cái riêng? Vận dụng ý nghĩa phương pháp luận trong giải quyết mối quan hệ trên để phân tích mối quan hệ giữa chủ nghĩa Mác-Lênin với thực tiễn cách mạng Việt Nam? | Myphamthucuc.vn
Câu 11. Tại sao phải thực hiện dạy học phân hóa? Chủ trương dạy học phân hóa trong CT mới có gì khác CT hiện hành? Những thuận lợi và khó khăn trong việc thực hiện dạy học phân hóa hiện và cách khắc phục? | Myphamthucuc.vn
Tư tưởng Đất Nước của Nhân dân trong Đất nước của Nguyễn Khoa Điềm
Các Kiểm Tra Hạn Sử Dụng Của Kem Chống Nắng Skin Aqua Nhật Bản
Bài thơ “Ngắm trăng” được sáng tác trong hoàn cảnh nào?
Câu hỏi ôn tập bài Sau phút chia li chọn lọc chi tiết
Phân tích tâm trạng nhân vật Liên khi chờ tàu năm 2023
Giới thiệu về Ngô Gia văn phái năm 2023
Kem Dưỡng Estee Lauder Thật Giả Qua Các Dung Tích, So Sánh Và Nhận Biết Serum Advance Night Repair
Nhân vật Mị sau khi về làm dâu nhà thống lí Pá Tra trong Vợ chồng A Phủ
Phân tích bức tranh tứ bình trong bài Nhớ rừng của Thế Lữ năm 2023
Viết thư cho Cô giáo cũ nhân ngày 20/11 năm 2023
Soạn bài Vừa nhắm mắt vừa mở cửa sổ
