Giải Toán 11: Bài 10 trang 114 SGK Hình học 11 | Myphamthucuc.vn
Bài 4: Hai mặt phẳng vuông góc
Bài 10 trang 114 SGK Hình học 11
Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a. Gọi O là tâm của hình vuông ABCD.
a) Tính độ dài đoạn SO.
b) Gọi M là trung điểm của đoạn SC. Chứng minh hai mặt phẳng (MBD) và (SAC) vuông góc với nhau.
c) Tính độ dài đoạn OM và tính góc giữa hai mặt phẳng (MBD) và (ABCD).
Lời giải
Hướng dẫn
a) Áp dụng định lý Pi-ta-go cho tam giác vuông.
b) Chứng minh BD ⊥ (SAC) và sử dụng lý thuyết: Nếu một đường thẳng vuông góc với một phẳng thì mọi mặt phẳng chứa đường thẳng này đều vuông góc mặt phẳng kia.
c) Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến.
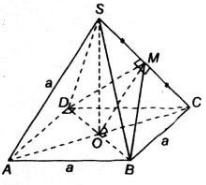
a) Theo giả thiết, S.ABCD là hình chóp đều nên ( tính chất hình chóp đều)
Đáy ABCD là hình vuông cạnh a nên
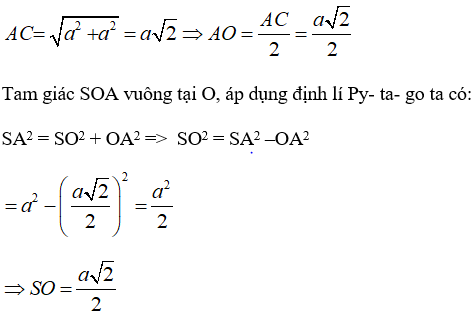
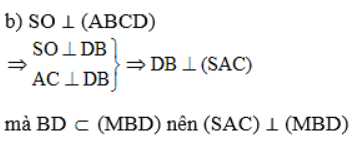
=> Góc giữa hai mặt phẳng (MBD) và (ABCD) là 45o
Xem toàn bộ Giải Toán 11: Bài 4. Hai mặt phẳng vuông góc
Có thể bạn quan tâm
Bài viết hay nhất
Các Kiểm Tra Hạn Sử Dụng Của Kem Chống Nắng Skin Aqua Nhật Bản
Câu hỏi ôn tập bài Sau phút chia li chọn lọc chi tiết
Bài thơ “Ngắm trăng” được sáng tác trong hoàn cảnh nào?
Phân tích tâm trạng nhân vật Liên khi chờ tàu năm 2023
Kem Dưỡng Estee Lauder Thật Giả Qua Các Dung Tích, So Sánh Và Nhận Biết Serum Advance Night Repair
Giới thiệu về Ngô Gia văn phái năm 2023
Nhân vật Mị sau khi về làm dâu nhà thống lí Pá Tra trong Vợ chồng A Phủ
Phân tích bức tranh tứ bình trong bài Nhớ rừng của Thế Lữ năm 2023
Viết thư cho Cô giáo cũ nhân ngày 20/11 năm 2023
Soạn bài Vừa nhắm mắt vừa mở cửa sổ
Chủ đề của truyện Tấm Cám là gì
Cách Vẽ Mặt Nạ Hình Con Vật Hươu Cho Bé, Cách Làm Mặt Nạ Hình Con Thỏ Chơi Trung Thu
Cách Dùng Kem Dưỡng Da Johnson Baby Nắp Xanh Có Tác Dụng Gì? Sử Dụng Ra Sao?
Câu hỏi bài Hai đứa trẻ chọn lọc