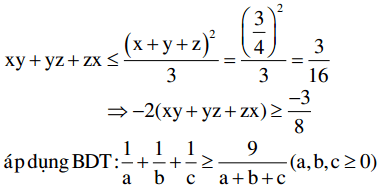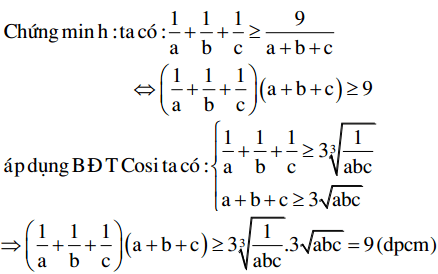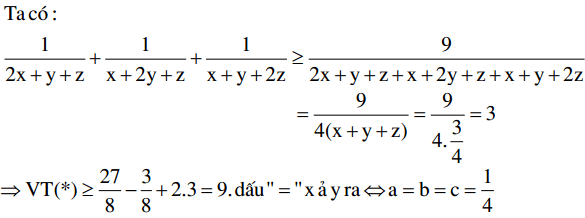Đáp án đề thi tuyển sinh lớp 10 môn Toán Sở GDĐT Hải Phòng (2018-2019) | Myphamthucuc.vn

Đáp án đề thi tuyển sinh lớp 10 môn Toán

Sở GDĐT Hải Phòng (2018-2019)

Câu 1:

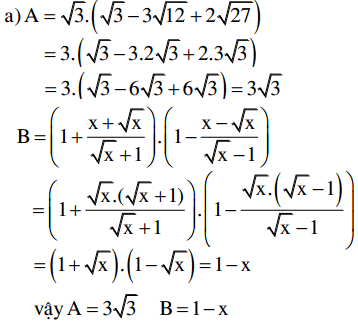
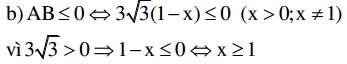
Kết hợp với đk x > 1

Câu 2: 

a)(d): y = ax + b song song với y = 2x -1 ⇒

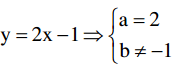
Vì (d): y = 2x + b cắt trục tung tại điểm có tung độ bằng 3

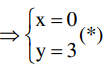
thay (*) vào (d) ⇒ 3 = 2.0 + b b = 3 (thỏa) vậy a = 2;b = 3

3x + J y + 6 = 11    f8x = 24

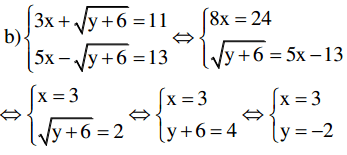
Vậy(x;y) = (3;-2)

Câu 3:

1.

a) Với m = 2, ptrình (*) thành: x² – 6x + 5 = 0 ⇒ x² – x – 5x + 5 = 0

⇔ x(x -1) – 5(x -1) = 0 ⇔ (x – 5)(x -1) = 0

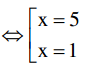
Vậy khi m = 2 thì 

b) x² – 2(m + 1)x + m² +1 = 0 (*) phương trình đã cho có hai nghiệm phân biệt ⇔ Δ’ > 0

⇔ (m +1)² – m² – 1 > 0 ⇔ m² + 2m + 1 – m² – 1 > 0 ⇔ 2m > 0 ⇔ m > 0

Áp dụng Vi et ta có:

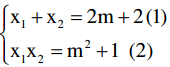
theo bài x₁ – 2x₂ = -1 (3)

Từ (1); (3) ta có hệ phương trình 

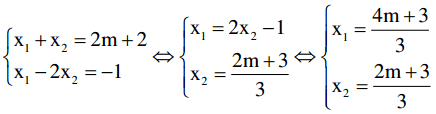
Thay vào (2) ta được:

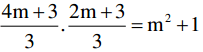
⇔ 8m² + 12m + 6m + 9 = 9m² + 9

⇔ m² + 18m = 0

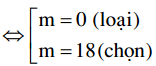
vậy m = 18 thì thỏa đề

2.

a) Gọi vận tốc của ô tô thứ nhất là x (km/h) (x > 0)

Thời gian ô tô đi hết quãng đường AB là: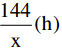 

Vận tốc của ô tô thứ 2 là: x + 6 (km/h)

Thời gian ô tô 2 đi hết quãng đường AB là: 

ô tô thứ nhất đi sớm hơn ô tô thứ hai 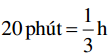   nên ta có phương trình

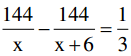
⇔ 3.144(x + 6) – 3.144x = x(x + 6)

⇔ x² + 6x – 2592 = 0

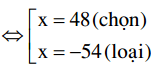
Vậy vận tốc của ô tô 1: 48 (km/h), vận tốc của ô tô 2: 48 + 6 = 54 (km/h)

b) Vì biển báo là 50km/h nên xe thứ hai vi phạm tốc độ do 54 > 50

Câu 4:

1.

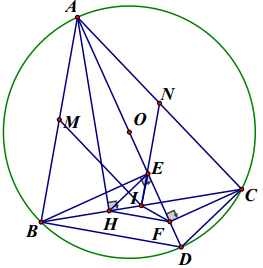
a) Xét tứ giác ABHE có : ∠AHB = ∠AEB (gt)

⇒ Hai điểm H và E cùng nhìn AB dưới 1 góc 90

⇒ Tứ giác ABHE là tứ giác nội tiếp đường tròn đường kính AB

b) Do tứ giác ABHE nội tiếp (cmt) ∠DEH = ∠ABC

mà ∠ABC = ∠ADC (hai góc nội tiếp cùng chắn AC) ⇒ ∠DEH = ∠ADC

mà hai góc này ở vị trí so le trong ⇒ HE //CD

c) Gọi M, N lần lượt là trung điểm AB, AC

M là tâm đường tròn ngoại tiếp tứ giác ABHE (cmt)

Ta có: IM làđường trung bình của tam giác ABC ⇒ IM// AC

Ta có IM // AC; HE //CD; AC ⊥ CD (góc nội tiếp chắn nửa đường tròn)

⇒ IM ⊥ HE

IM là đường trung trực của HE ⇒ IH = IE (1)

Chứng minh tương tự ta có

Xét tứ giác AHFC có: ∠AHC = ∠AFC = 90 (gt) AHFC nội tiếp đường tròn đường kính AC, tâm N ⇒ ∠FHC = ∠CAD mà ∠CAD = ∠CBD (cùng chắn cung CD) ⇒ ∠FHC = ∠CBD

mà hai góc này ở vị trí đồng vị HF //BD

IN là đường trung bình ΔABC ⇒ IN // AB

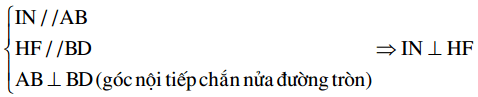
IN là đường trung trực của HF ⇒ IH = IF (2)

từ(1) và(2) ⇒ IE = IF.

2.

Gọi l làđộ dài đường sinh của hình nón. áp dụng định lý Pytago ta có:

⇒ Diện tích xung quanh của h X nh nón là

S_xq = πrl = π12.20 = 240π (cm²)

Diện tích đáy của hình nón là S_đ = πr² = 144π (cm²)

Vậy diện tích toàn phần của h x nh nón là: S_tp = S_xq + S_d = 240π +144π = 384π (cm²)

Bài 5:

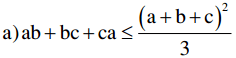
3(ab + bc + ca) ≤ (a + b + c)²

3(ab + bc + ca) ≤ a² + b² + c² + 2ab + 2bc + 2ca

a² + b² + c² – ab – bc – ca ≥ 0

2a² + 2b² + 2c² — 2ab — 2bc — 2ca ≥ 0

(a² – 2ab + b²) + (b² -2bc + c²) + (c² – 2ca + a²) ≥ 0

(a – b)² + (b – c)² + (c – a)² ≥ 0 (luôn luôn đúng) ⇒ Đpcm

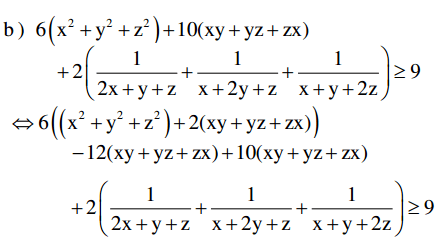
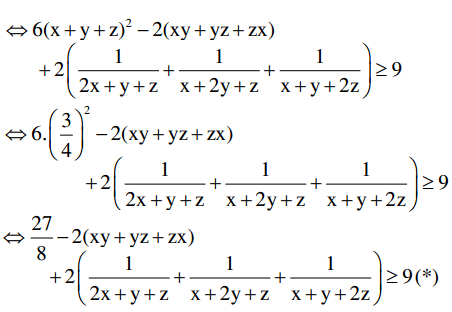
Áp dụng BĐT ở ý a, ta có: