Bài 70 trang 141 SGK Toán 7 tập 1 | Myphamthucuc.vn
Ôn tập chương 2 – Phần Hình Học
Bài 70 (trang 141 SGK Toán 7 Tập 1)
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M trên tia đối của tia CB lấy điểm N sao cho BM = CN.
a) Chứng minh rằng tam giác AMN là tam giác cân
b) Kẻ BH ⊥ AM, kẻ CK ⊥ Chứng minh rằng BH = CK
c) CMR AH = AK
d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì ? Vì sao
e) Khi góc BAC = 60ovà BM = CN = BC hãy tính số đo các góc của tam giác AMN và xác định dạng của tam giác OBC
Lời giải: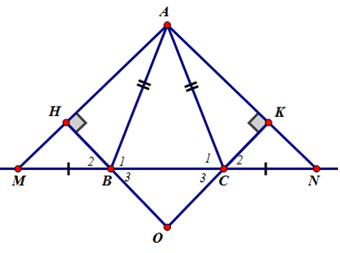
a) Ta có ΔABC cân tại A suy ra
Lại có :
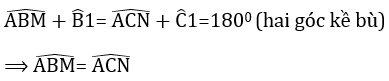
– Xét ΔABM và ΔACN có
AB = AC (Do ΔABC cân tại A).
BM = CN(gt)
Nên ΔABM = ΔACN (c.g.c)
⇒ AM = AN (2 góc tương ứng)
⇒ ΔAMN cân tại A.
b) Xét 2 tam giác vuông BHM và CKN có
BM = CN (gt)
Nên ΔBHM = ΔCKN (cạnh huyền – góc nhọn)
⇒ BH = CK (2 cạnh tương ứng)
c) Theo câu b ta có ΔBHM = ΔCKN ⇒HM = KN (2 góc tương ứng)
Mà AM = AN ⇒ AM –MH = AK – KN hay AH = AK.
d) ΔBHM = ΔCKN
Vậy tam giác OBC là tam giác cân tại O.
e) Khi góc BAC = 60º và BM = CN = BC
Tam giác cân ABC có góc BAC = 60º nên là tam giác đều
⇒ AB = BC và góc B1 = 60º
Ta có: AB = CB, BC = BM (gt) ⇒ AB = BM ⇒ ΔABM cân ở B ⇒ 
Áp dụng tính chất góc ngoài trong ΔBAM:
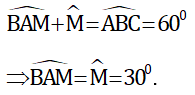
Tương tự ta có
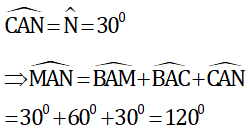
Tam giác cân OBC có góc B3=60º nên ΔOBC là tam giác đều.
Xem toàn bộ Giải Toán 7: Ôn tập chương 2 – Phần Hình học
Có thể bạn quan tâm
Bài viết hay nhất
Câu 10. Tại sao phải dạy học tích hợp? Chủ trương dạy học tích hợp có gì mới? Những thuận lợi, khó khăn và cách khắc phục khi thực hiện dạy học tích hợp? | Myphamthucuc.vn
Mối quan hệ biện chứng giữa cái chung và cái riêng? Vận dụng ý nghĩa phương pháp luận trong giải quyết mối quan hệ trên để phân tích mối quan hệ giữa chủ nghĩa Mác-Lênin với thực tiễn cách mạng Việt Nam? | Myphamthucuc.vn
Câu 11. Tại sao phải thực hiện dạy học phân hóa? Chủ trương dạy học phân hóa trong CT mới có gì khác CT hiện hành? Những thuận lợi và khó khăn trong việc thực hiện dạy học phân hóa hiện và cách khắc phục? | Myphamthucuc.vn
Tư tưởng Đất Nước của Nhân dân trong Đất nước của Nguyễn Khoa Điềm
Các Kiểm Tra Hạn Sử Dụng Của Kem Chống Nắng Skin Aqua Nhật Bản
Bài thơ “Ngắm trăng” được sáng tác trong hoàn cảnh nào?
Câu hỏi ôn tập bài Sau phút chia li chọn lọc chi tiết
Phân tích tâm trạng nhân vật Liên khi chờ tàu năm 2023
Giới thiệu về Ngô Gia văn phái năm 2023
Kem Dưỡng Estee Lauder Thật Giả Qua Các Dung Tích, So Sánh Và Nhận Biết Serum Advance Night Repair
Nhân vật Mị sau khi về làm dâu nhà thống lí Pá Tra trong Vợ chồng A Phủ
Phân tích bức tranh tứ bình trong bài Nhớ rừng của Thế Lữ năm 2023
Viết thư cho Cô giáo cũ nhân ngày 20/11 năm 2023
Soạn bài Vừa nhắm mắt vừa mở cửa sổ
