Bài 56 trang 63 SGK Toán 9 tập 2 – TopLoigiai | Myphamthucuc.vn

Ôn tập chương 4 (Câu hỏi – Bài tập)

Bài 56 (trang 63 SGK Toán 9 tập 2)

Giải các phương trình:

a) 3x⁴ – 12x² + 9 = 0;

b) 2x⁴+ 3x²– 2 = 0;

c) x⁴+ 5x²+ 1 = 0.

Lời giải

Cả ba phương trình trên đều là phương trình trùng phương.

a) 3x⁴– 12x²+ 9 = 0 (1)

Đặt x² = t, t > 0.

(1) trở thành: 3t² – 12t + 9 = 0 (2)

Giải (2):

Có a = 3; b = -12; c = 9

⇒ a + b + c = 0

⇒ (2) có hai nghiệm t₁ = 1 và t₂ = 3.

Cả hai nghiệm đều thỏa mãn điều kiện.

+ t = 3 ⇒ x² = 3 ⇒ x = ±√3.

+ t = 1 ⇒ x² = 1 ⇒ x = ±1.

Vậy phương trình có tập nghiệm

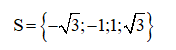
b) 2x⁴+ 3x²– 2 = 0 (1)

Đặt x² = t, t > 0.

(1) trở thành: 2t² + 3t – 2 = 0 (2)

Giải (2) :

Có a = 2 ; b = 3 ; c = -2

⇒ Δ = 3² – 4.2.(-2) = 25 > 0

⇒ (2) có hai nghiệm

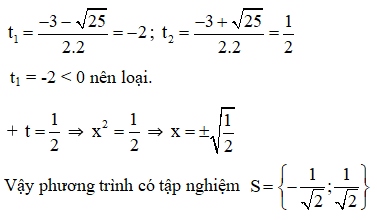
c) x⁴+ 5x²+ 1 = 0 (1)

Đặt x² = t, t > 0.

(1) trở thành: t² + 5t + 1 = 0 (2)

Giải (2):

Có a = 1; b = 5; c = 1

⇒ Δ = 5² – 4.1.1 = 21 > 0

⇒ Phương trình có 2 nghiệm:

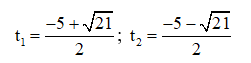
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.

Vậy phương trình (1) vô nghiệm.

Tham khảo toàn bộ: Giải Toán 9