Bài 5. Hình chiếu trục đo – TopLoigiai | Myphamthucuc.vn
Bài 5: Hình chiếu trục đo
Tóm tắt lý thuyết
I – KHÁI NIỆM
1. Thế nào là hình chiếu trục đo?
a. Cách xây dựng
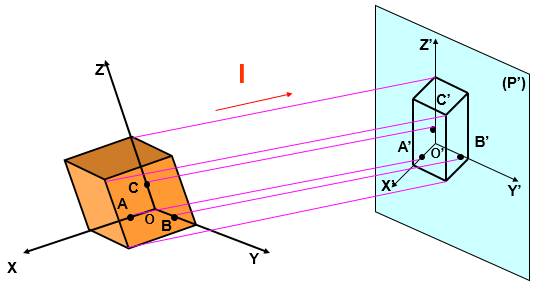
Hình 5.1 Phương pháp xây dựng hình chiếu trục đo
– Một vật thể V gắn vào hệ trục toạ độ vuông góc OXYZ với các trục toạ độ đặt theo ba chiều dài, rộng, cao của vật thể;
– Chiếu vật thể cùng hệ trục toạ độ vuông góc lên mặt phắng hình chiếu P’ theo phương chiếu l (l không song song với P’ và bất cứ trục toạ độ nào). Kết quả thu được V’ trên P’ – đó chính là hình chiếu trục đo của V.
b. Định nghĩa
Hình chiếu trục đo là hình biểu diễn không gian ba chiều của vật thể, được xây dựng bằng phép chiếu song song.
2. Các thông số của hình chiếu trục đo
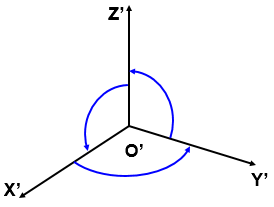
Hình 5.2. Các góc trục đo
a. Góc trục đo
Trong phép chiếu trên:
O’X’; O’Y’ O’Z’: gọi là các trục đo
Các góc X’O’Z; X’O’Y’; Y’O’Z’: Các góc trục đo
b. Hệ số biến dạng
– Hệ số biến dạng là tỉ số độ dài hình chiếu của một đoạn thẳng nằm trên trục toạ độ với độ dài thực của đoạn thẳng đó.
– Trong đó:
II – HÌNH CHIẾU TRỤC ĐO VUÔNG GÓC ĐỀU
1. Thông số cơ bản
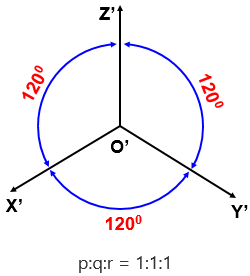
Hình 5.3. Góc trục đo hình chiếu trục đo vuông góc đều
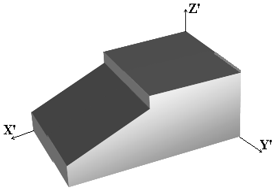
Hình 5.4. Hình biểu diễn hình chiếu trục đo vuông góc đều
a. Góc trục đo
b. Hệ số biến dạng
p = q = r = 1
2. Hình chiếu trục đo của hình tròn
– Hình chiếu trục đo vuông góc đều của một hình tròn nằm trong các mặt phẳng song song với các mặt toạ độ là một hình Elip theo các hướng khác nhau.
– Trong hình chiếu trục đo vuông góc đều tỉ số biến dạng được quy ước: Nếu vẽ theo hệ số biến dạng quy ước (p=q=r=1) thì các elip đó có trục dài bằng 1,22d và trục ngắn bằng 0,71d (d là đường kính của hình tròn)
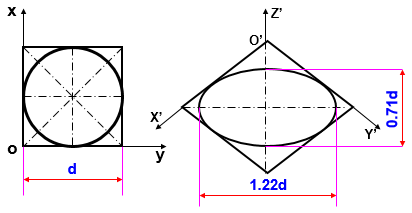
Hình 5.5. Góc trục đo hình chiếu trục đo của hình tròn
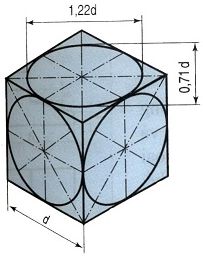
Hình 5.6. Hướng các elip
Vì vậy: Hình chiếu trục đo vuông góc đều được ứng dụng để biểu diễn các vật thể có các lỗ tròn.
III – HÌNH CHIẾU TRỤC ĐO XIÊN GÓC CÂN
1. Thông số cơ bản
a. Góc trục đo
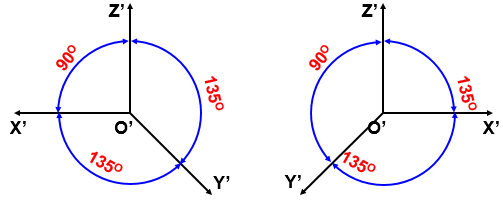
Hình 5.7. Góc trục đo hình chiếu trục đo xiên góc cân
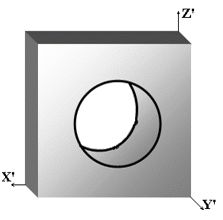
Hình 5.8. Hình biểu diễn hình chiếu trục đo xiên góc cân
b. Hệ số biến dạng
p = r = 1; q = 0.5
IV – CÁCH VẼ HÌNH CHIẾU TRỤC ĐO
Các bước vẽ hình chiếu trục đo:
Bước 1. Chọn cách vẽ phù hợp với hình dạng vật thể
Bước 2. Đặt các trục toạ độ theo các chiều dài, rộng, cao của vật thể
Ví dụ: Vẽ hình chiếu trục đo của một cái đe từ các hình chiếu vuông góc của nó
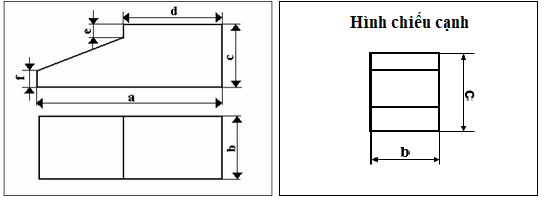
Hình 5.9. Các hình chiếu của vật thể
Bước 1. Chọn mặt phẳng O’X’Z’ làm mặt phẳng cơ sở thứ nhất để vẽ một mặt của vật thể theo các kích thước đã cho
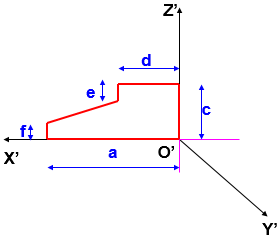
Hình 5.10. Hình chiếu trục đo xiên góc cân của cái đe với mặt phẳng cơ sở thứ nhất
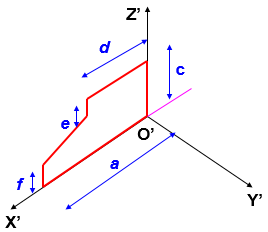
Hình 5.11. Hình chiếu trục đo vuông góc đều của cái đe với mặt phẳng cơ sở thứ nhất
Bước 2. Dựng mặt phẳng cơ sở thứ hai O1X1Z1 song song và cách mặt thứ nhất một khoảng để vẽ mặt còn lại của vật thể.
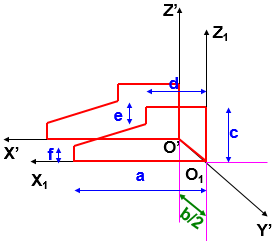
Hình 5.12. Hình chiếu trục đo xiên góc cân của cái đe với mặt phẳng cơ sở thứ hai
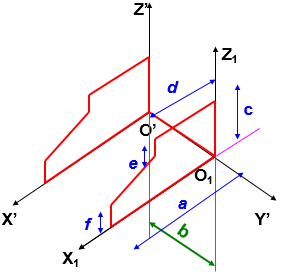
Hình 5.13. Hình chiếu trục đo vuông góc đều của cái đe với mặt phẳng cơ sở thứ hai
Bước 3. Nối các đỉnh còn lại của hai mặt vật thể và xóa các đường thừa, đường khuất ta thu được hình chiếu trục đo của vật thể.
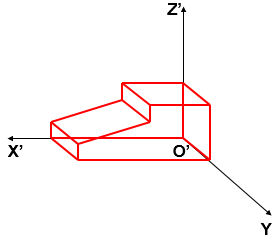
Hình 5.14. Hình chiếu trục đo xiên góc cân của cái đe
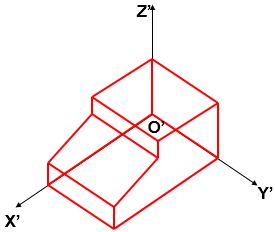
Hình 5.15. Hình chiếu trục đo vuông góc đều của cái đe
Tổng kết
Sau khi học xong Bài 5: Hình chiếu trục đo, các em cần nắm vững các nội dung trọng tâm:
– Thế nào là hình chiếu trục đo?
– Các thông số của hình chiếu trục đo
– Các thông số cơ bản của hình chiếu trục đo vuông góc đều và hình chiếu trục đo xiên góc cân
– Cách vẽ hình chiếu trục đo
Có thể bạn quan tâm
Bài viết hay nhất
Câu 10. Tại sao phải dạy học tích hợp? Chủ trương dạy học tích hợp có gì mới? Những thuận lợi, khó khăn và cách khắc phục khi thực hiện dạy học tích hợp? | Myphamthucuc.vn
Mối quan hệ biện chứng giữa cái chung và cái riêng? Vận dụng ý nghĩa phương pháp luận trong giải quyết mối quan hệ trên để phân tích mối quan hệ giữa chủ nghĩa Mác-Lênin với thực tiễn cách mạng Việt Nam? | Myphamthucuc.vn
Câu 11. Tại sao phải thực hiện dạy học phân hóa? Chủ trương dạy học phân hóa trong CT mới có gì khác CT hiện hành? Những thuận lợi và khó khăn trong việc thực hiện dạy học phân hóa hiện và cách khắc phục? | Myphamthucuc.vn
Tư tưởng Đất Nước của Nhân dân trong Đất nước của Nguyễn Khoa Điềm
Các Kiểm Tra Hạn Sử Dụng Của Kem Chống Nắng Skin Aqua Nhật Bản
Bài thơ “Ngắm trăng” được sáng tác trong hoàn cảnh nào?
Câu hỏi ôn tập bài Sau phút chia li chọn lọc chi tiết
Phân tích tâm trạng nhân vật Liên khi chờ tàu năm 2023
Giới thiệu về Ngô Gia văn phái năm 2023
Kem Dưỡng Estee Lauder Thật Giả Qua Các Dung Tích, So Sánh Và Nhận Biết Serum Advance Night Repair
Nhân vật Mị sau khi về làm dâu nhà thống lí Pá Tra trong Vợ chồng A Phủ
Phân tích bức tranh tứ bình trong bài Nhớ rừng của Thế Lữ năm 2023
Viết thư cho Cô giáo cũ nhân ngày 20/11 năm 2023
Soạn bài Vừa nhắm mắt vừa mở cửa sổ
