Công thức tính đường chéo hình bình hành | Myphamthucuc.vn
Cách tính đường chéo hình bình hành cũng là một trong số các kiến thức cần thiết và quan trọng đối với các em học sinh trong quá trình giải toán hình học các lớp. Vậy em đã biết cách làm các dạng bài tập này hay chưa, nếu em vẫn còn đang loay hoay chưa biết làm như thế nào, vậy em có thể tham khảo bài viết của chúng tôi.
Hình bình hành gồm hai đường chéo và chúng cũng có cách tính riêng, các bạn cùng theo dõi bài viết hướng dẫn chi tiết dưới đây để biết cách làm bài tập tính toán đường chéo hình bình hành.
Công thức tính đường chéo hình bình hành
Định nghĩa hình bình hành
HBH là tứ giác có các cạnh đối song song
Ví dụ:
Ta có AB // CD, AD // BC thì ABCD là HBH.
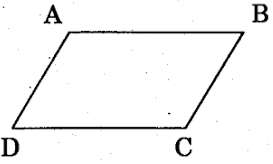
HBH ABCD
Nhận xét: HBH là hình thang có hai cạnh bên song song.
Đặc Điểm Đường Chéo Của Hình Bình Hành
– Hai đường chéo cắt nhau tại trung điểm mỗi đường.
– Độ dài các đường chéo của hình bình hành không bằng nhau và không vuông góc với nhau.
– Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
– Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
Công Thức Tổng Quát Tính Đường Chéo Của Hình Bình Hành
Muốn tính đường chéo của hình bình hành, ta áp dụng công thức như sau:
![]()
Trong đó:
d1,2: Đường chéo 1 và đường chéo 2 của hình bình hành
a, b: Độ dài các cạnh hình bình hành
α1, α2: là các góc được tạo bởi 2 cạnh kề nhau của hình bình hành, α1 + α2 = 180o.
Trường hợp đặc biệt công thức tính đường chéo hình thoi
Để đưa ra được công thức tính đường chéo hình thoi, chúng ta xét ví dụ sau đây:
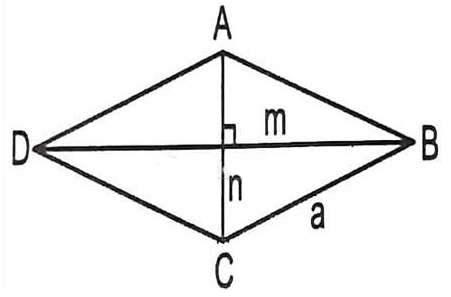
Giả sử ta cần tính độ dài đường chéo hình thoi ABCD có cạnh a và một góc ABC = 60 độ -> công thức tính đường chéo hình thoi trong trường hợp này như thế nào?
Lời giải:
Vì ABCD là hình thoi nên các cạnh đều bằng a.
Xét tam giác ABC có: AB = BC = a
Lại có: ABC = 60 độ => Tam giác ABC là tam giác đều cạnh a.
=> AB = AC = BC = a
=> Độ dài đường chéo hình thoi chính là AC = BD = a.
Bài toán cho biết hai cạnh và độ dài một đường chéo hình bình hành, tính đường chéo còn lại.
*Xét Bài Toán : Hình bình hành ABCD có AB = 6 cm, BC = 7 cm, BD = 8 cm. Tính AC.
Hướng dẫn cách làm:
– Gọi I là giao điểm của hai đường chéo AC và BD => AI là đường trung tuyến của tam giác ABD
– Tính độ dài AI: Áp dụng công thức tính đường trung tuyến
=> AI2 = (AB2 + AD2) : 2 – (BD2 : 4)
– Tính độ dài AC: Vì I là trung điểm của AC nên AC = 2.AI
– Kết luận.
* Các bạn dựa theo gợi ý như trên, thay số và tự giải bài tập này.
Bài toán mở rộng liên quan đến đường chéo hình bình hành
* Xét Bài Toán Sau: Chứng minh rằng tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường là hình bình hành.
Hướng dẫn cách làm: Đối với bài toán này, bạn thực hiện các bước như sau:
Xét tứ giác ABCD, gọi O là giao điểm của hai đường chéo AC và BD
=> OA = OC
OB = OD
Xét tam giác OAD và tam giác OBC có:
OA = OC
OB = OD
góc AOD = góc BOC (do tính chất đối đỉnh)
=> Tam giác OAD = tam giác OBC
=> góc OAD = góc OBC
Do hai góc trên là hai góc so le trong nên
AD // BC
mà AD = BC (do hai tam giác bằng nhau)
=> Tứ giác ABCD là hình bình hành.
Trên đây là cách tính đường chéo hình bình hành chúng tôi giới thiệu đến độc giả, để làm phần bài tập này tốt, các bạn nhớ học thuộc lòng công thức cũng như nắm vững cách làm để hoàn thành tốt nhất các bài tập này và vận dụng vào các bài toán tính diện tích hình bình hành nhé. Các bậc cha mẹ học sinh cũng có thể tham khảo tài liệu của chúng tôi để hướng dẫn con mình học bài ở nhà hiệu quả hơn.



















